GRAFOS I - Mates

(Todas las representaciones de grafos en esta entrada están realizadas en un programa propio que será publicado próximamente junto a otras cosas para poder ser usado por todo el mundo)

"Puntos y rayas" diréis algunos. Otros, especificaréis más y diréis "Matemáticas con puntos y rayas". Y otros, los más expertos en el tema diréis "Una forma de ver las matemáticas tan simple y tan compleja como la que más a la vez". Más o menos eso es lo más exacto a la hora de hablar sobre grafos. Pero... ¿Realmente no podemos hablar más sobre ello? En la entrada de hoy hablaremos sobre grafos y algunas de sus utilidades más famosas y/o bonitas.

Antes de comenzar, quiero citar a la gran Clara Grima, ya que ella es la gran divulgadora de los grafos. Si queréis saber algo más que lo que vamos a hablar hoy (ya que hablaremos muy poquito), te recomiendo en exceso leer EN BUSCA DEL GRAFO PERDIDO de, quien ya habíamos comentado antes, la gran Clara Grima.

Una vez terminada toda esta explicación, comenzaremos con una pequeña introducción a la Teoría de Grafos. Comencemos por los elementos de un grafo, un grafo está formado por sus nodos o vértices (representados con puntos) y por sus aristas (representadas con rayas) que unen los nodos. Contamos con dos tipos de grafos: los grafos dirigidos y los grafos no dirigidos. De esto hablaremos un poco más adelante, pero os puedo adelantar que en un grafo dirigido, un punto está unido con otro que no tiene por qué estar necesariamente unido con dicho punto. Y luego tenemos los grafos no dirigidos, los puntos que están unidos entre sí. En este último tipo de grafo, obligatoriamente, si el punto A está unido con el punto B, el punto B estará conectado con el punto A. El siguiente elemento a conocer es la valencia de un grafo, representada con la letra . La valencia hace referencia a la cantidad de conexiones que tiene un vértice. Por ejemplo, un vértice conectado a otros dos vértices, se dice que su valencia es igual a 2.

Nos falta lo último en cuanto a teoría se refiere. Un grafo pueden ser representados gráficamente o, también, mediante un matriz de adyacencia. Este último representa mediante unos y ceros un grafo, ¿Cómo? Muy fácil. Fijémonos en este grafo, en el grafo de portada:

Vamos a centrarnos en las conexiones de cada vértice:
1 está conectado con 2, 3 y 4.

2 está conectado con 1 y 3.

3 está conectado con 1 y 2.

4 está conectado con 1.

Vamos a hacer una tabla donde los elementos verticales serán los mismo que los horizontales, los nombres de los vértices.

Vamos a representar en ella las conexiones de los distintos vértices. Lo primero que haremos será poner un guion en las casillas que conectan el mismo número ya que sabemos que el mismo vértice no puede estar conectado.

Ahora comenzaremos con las conexiones del vértice 1. Recordemos que el vértice 1 estaba conectado con todos los vértices menos consigo mismo. Por lo que, pondremos un SÍ en todas las casillas del 1. Pero, aquí nos debemos fijar. Ya que debemos ver que tanto en vertical como en horizontal lo tenemos que representar.

Continuamos con el segundo vértice. Este vértice está conectado con el vértice 1 (ya está mostrado en la tabla) y con el 3. Mostraremos su conexión con el 3.

Continuamos (y terminamos) con el tercer vértice. Este vértice está conectado solamente con los vértices 1 y 2. Los cuales ya están mostrados en la tabla.

Y, efectivamente, como habrás podido adivinar, no nos hace falta marcar los vértices del último vértice para saberlos. 

Ahora, si queremos representar esto de una forma más matemática, cambiaremos los síes por unos y los noes por ceros.

Y ahora sí, tendríamos terminado nuestro matriz de adyacencia.

A continuación, comenzaremos con algunos problemas divertidos usando solo eso, grafos. (Inspirado en Clara Grima)

LA FIESTA DE AMIGOS

En una fiesta sueles saludar al resto de amigos que vienen, ¿no? Supongamos que sí. A esta fiesta se viene por parejas. Y han venido un total de 5 parejas (10 amigos). Jose y Elia van juntos a la fiesta. Hay dos maneras de saludar:
-Con besos.

-Con un apretón de manos.

Jose recogió unos papeles donde cada uno ha escrito a cuántas personas les dio la mano al llegar. Haciendo un recuento de los papeles, Jose llega a la conclusión de que hay 9 respuestas diferentes, sabiendo esto, Jose se pregunta, ¿A cuántas personas habrá dado la mano Elia?

Puede parecer un problema muy complejo de resolver, pero vas a ver cómo, mediante grafos, es mucho más fácil de los que piensas.

Antes de meternos con los grafos, pensemos. Una persona no saluda a su pareja, por lo que, nadie habrá saludado a 9 personas, por lo que, nadie habrá dado la mano a 9 personas. Así que, ya sabemos que solamente puedes dar la mano a 8 personas como mucho. Sabiendo que hay nueve respuestas diferentes, habrás podido dar la mano a 0, 1, 2, 3, 4, 5, 6, 7 u 8 personas.

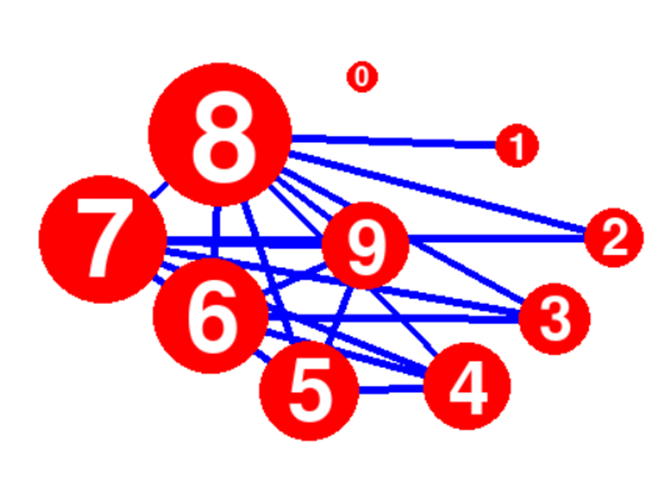
Ahora sí, vamos a representarlo en un grafo. Primero dibujamos el grafo con 10 vértices representando a 10 personas (Jose + amigos). El número en cada grafo representa la respuesta de cada persona. Es decir, el grafo llamado 1 ha dado la mano a 1 persona, el 2 a 2... Cabe decir que el número 9 representa a Jose aunque no tenga 9 conexiones obligatoriamente..

Sabiendo que el número 8 ha dado la mano a 8 personas, solo tenemos que pensar un poco. Lo uniremos con todos los vértices menos con el cero, ya que no tendrá conexiones.

(El cambio de tamaño en función de la valencia del vértice es una de las funciones más llamativas de este programa. No te lo pierdas cuando esté disponible)

Continuaremos por el siguiente vértice, por el 7. Haremos lo mismo, solo que, en vez de unirlos a todos, hemos de saber que el 7 y el 8 ya están unidos, así que restaremos una unión, ya van 6. Después que el 1 ya tiene una unión, así que no le hará falta más conexiones. Así que habremos de unir el 7 con el 6, el 5, el 4, el 3, el 2 y con Jose. Antes de hacerlo vamos a percatarnos de una cosa. El 8 y el 0 son pareja. Ya que no se han saludado y, normalmente, una pareja no se saluda en una fiesta. Así que ya sabemos una pareja.

Vamos a por el vértice 6. Este vértice lo tendremos que unir con el 3, el 4, el 5 y con Jose. Ya que ya está unido con el 7 y 8 (2) y no se puede unir ni con el 0 (tiene 0 conexiones), ni con el 1 (ya tiene una conexión), ni con 2 (ya tiene sus dos conexiones. Debido a esto, podemos saber que el 7 y el 1 son pareja, porque no se ha unido con él y el otro con el que no se unió (el 0) ya es pareja del 8.

Repetiremos esto con el 5 también.

Ya tenemos nuestro grafo terminado.

El 6 será pareja del 2 y el 5 del 3.

Por lo que, sabiendo esto, el 9 (Jose) será pareja del 4. Así que, Elia es el número 4. Por lo que, la pareja de Jose ha dado un total de cuatro apretones de mano.

Al final no es tan difícil, ¿no?

Vamos con el segundo.

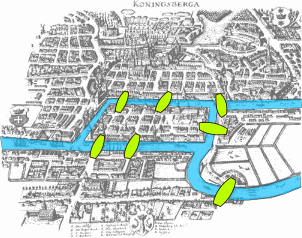
PUENTES DE KÖNIGSBERG

Perfecto, ahora que ya hemos comenzado con la teoría de grafos, continuaremos con otro problema muy chulo en el que son de una grandísima utilidad.

Partimos de este mapa que es el mapa de Königsberg en la época de Euler.

Ahora, vamos a integrar un grafo en el, representando cada lugar después del puente:

Sé que de primeras puede no parecer algo claro. Pero imaginemos que cada vértice es un lugar después del puente. De cada vértice salen tantas aristas como puentes lo conecten con otro lugar (otro vértice). En ocasiones salen dos aristas en dirección al mismo vértice. Esto es porque dos lugares están conectados por más de un puente.

La pregunta del millón es la siguiente: ¿se puede recorrer todos los puentes y volver al lugar de partida recorriendo cada uno tan solo una vez?

Aquí fue cuando Leonhard Euler resolvió este problema. Y eso originó lo que hoy conocemos como el Teorema de Euler.

Se dice que un grafo es euleriano si se puede recorrer (empezando y terminando en el mismo vértice) sin repetir aristas.

Hay una manera de saber si un grafo es euleriano: si el número de aristas que salen de cada vértice es un número par, entonces el grafo es euleriano.

Y un grafo tiene un camino euleriano (empieza en un vértice, termina en otro distinto, pero nunca ha repetido ningún vértice y ha recorrido todo el grafo) si solo tiene dos vértices de los que sale un número impar de aristas.

Sabiendo esto, ya podemos resolver el problema anteriormente mencionado. Si vemos las valencias de los vértices, vemos que todos los vértices tienen una valencia impar (3 o 5, dependiendo de él). Por lo que, este grafo no es euleriano y tampoco tiene un camino euleriano.

Vamos a probar ahora con este grafo:

Las valencias de los vértices son 2 o 3, dependiendo del que sea. Pero, solo tenemos 2 que tengan valencia 3, por lo que, es un grafo con camino euleriano. Tiene dos vértices de los que sale un número impar de aristas.

Si te ha gustado, agradecería que lo compartieras para seguir creciendo. ¡Muchas gracias por leer!