FIBONACCI, MÁS QUE UN MATEMÁTICO - Mates, Geogebra y Python

el

 

Hoy hablaremos sobre el matemático Leonardo de Pisa, más conocido como Fibonacci.
Fibonacci inventó una sucesión, la que pasó a llamarse sucesión de Fibonacci. También inventó el sistema de numeración decimal que hoy todos conocemos.
Antes de comenzar será importante conocer el número phi Φ (también denominado número áureo o número de oro). Este número es aproximadamente igual a 1,618033. Es un número irracional, es decir, no tiene fin. Sus seis primeras cifras decimales son 6, 1, 8, 0, 3, y 3. Este número tiene mucho que ver con la sucesión de Fibonacci.

LA SUCESIÓN DE FIBONACCI

   1, 1, 2, 3, 5, 8, 13, 21, 55...
Efectivamente, esto es la sucesión de Fibonacci, pero, ¿Qué oculta?

Fibonacci descubrió esta sucesión debido a un problema de conejos:
Si tenemos en cuenta que cada par de conejos se reproduce mensualmente cuando consiguen la madurez (a partir de su segundo mes de vida), y cada mes crían a dos nuevos conejos...

1º mes: nace el primer par de conejos.

2º mes: 1 par de conejos.

3º mes: el primer par de conejos ya ha conseguido la madurez, por lo tanto, tendremos ya 2 pares de conejos.

4º mes: el primer par de conejos continúa pariendo, mientras que el segundo par continúa madurando... Por lo tanto, tendremos 3 pares de conejos.

5º mes: el segundo par de conejos consigue la madurez, por lo tanto, tendremos dos nuevos pares (por parte del primer par y del segundo par). Por lo que, tendremos un total de 5 pares de conejos.

6º mes: el tercer par consigue la madurez, por lo tanto, tendremos tres nuevos pares (por parte del primer par, del segundo par y del tercer par). Por lo que, tendremos un total de 8 pares de conejos.

7º mes: el cuarto y el quinto par consiguen la madurez (ya que nacieron juntos en el 5º mes, hace dos meses), por lo tanto, tendremos cinco nuevos pares (por parte del primer par, del segundo, del tercero, del cuarto y del quinto). Por lo que, tendremos un total de 13 pares de conejos.

Podríamos seguir, pero... ¿Veis a lo que me quiero referir? A través de este problema de conejos se puede ver la sucesión de Fibonacci, y se dice, que así fue como la descubrió, pero... ¡Eso no es todo! Es más, ¡esto no es ni una pizca de lo que vamos a hablar hoy!

JUGANDO CON LA SUCESIÓN

Volvemos a la sucesión: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55... Vamos a jugar un poco con ella. Lo primero que haremos será designar una letra a cada número: a = 1, b = 1, c = 2, d = 3, e = 5...
Teniendo estas letras ya asignadas podremos comenzar con nuestros juegos:

-La regla más básica de la sucesión de Fibonacci es que un número es igual a la suma de los dos anteriores. Es decir, c = a + b, e = c + d... Para verlo mejor, podemos decir que 2 es igual a 1 + 1, que 5 es igual a 2 + 3...

-Debido a la "prueba de la resta" y a la anterior regla, tenemos otra regla... Cualquier número colocado en posición par de la sucesión es igual a la resta del número inmediatamente posterior menos el número inmediatamente inferior. Pongamos un ejemplo: 8 = 13 - 5. Esto es muy fácil, ¿no? Pues no perdamos más tiempo en ello.

-Cualquier número en posición impar de la sucesión elevado al cuadrado es igual al producto del número inmediatamente inferior y el número inmediatamente superior más 1. Pongamos unos ejemplos: c^2 = b * d - 1. Veámoslo mejor usando números reales: 2^2 = 1 * 3 + 1. Recordemos que 2 al cuadrado es lo mismo que 4, y que 1 * 3 es 3, si le sumamos 1... tenemos 4 también. Pongamos otro ejemplo: 5^2 = 3 * 8 + 1. Recordemos que 5 al cuadrado es 25 y que 3 por 8 es 24, y si le sumamos 1... ¡Nos da también 25! Así que, esta es otra regla que se cumple. Esto también se cumple con números pares, pero de manera distinta.

-Con referencia en la regla anterior, cualquier número en posición par de la sucesión elevado al cuadrado más uno es igual al producto inmediatamente anterior y el número inmediatamente posterior. Pongamos un ejemplo: b^2+1 = a*c. Veámoslo mejor usando números: 1^2+1 = 1*2. Como todos sabemos, 1 al cuadrado es 1, si le sumamos 1, será 2 en total. Mientras que 1 por 2 es 2. Por lo tanto... ¡Tendríamos otra regla! Pero, para comprobarlo haremos otro ejemplo: 3^2+1 = 2*5. Todos sabemos que 3 al cuadrado es 9, si le sumamos 1, 10 en total. Mientras que 2 por 5 es 10. Oficialmente, ¡esta regla se cumple!

-Si vamos dividiendo cada número por el anterior sucesiva y progresivamente, conseguiremos acercarnos cada vez más al famoso número phi. Probemos: 1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 = 1,66...; 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,6153...; 34/21 = 1,619...; 55/34 = 1,617...; 89/55=1,61818...
Como podemos observar, cada división nos acercamos más al número phi.

¿Mola? ¿A que sí? ¡Pues continuemos porque no hemos terminado!

¿DÓNDE ESTÁ LA SUCESIÓN DE FIBONACCI?

-Papá, ¿para qué sirven las mates? Si son aburridísimas...
-Si yo te contara, hijo...

Y efectivamente, las matemáticas están presentes hasta... ¡en la naturaleza! Y... flipad, ¡en el logo de Apple!



Alucinad, el logo de Apple ha sido diseñado utilizando las proporciones áureas (sucesión de Fibonacci). Podemos observar que en el centro de la manzana hay una circunferencia de radio 13, y a partir de ella, se crea el resto. Podemos ver cómo es todo simétrico y hasta los mordiscos han sido hechos con circunferencias pertenecientes a la sucesión de Fibonacci. 
Observadlo, volved a observarlo y así constantemente, ¡ES ALUCINANTE!

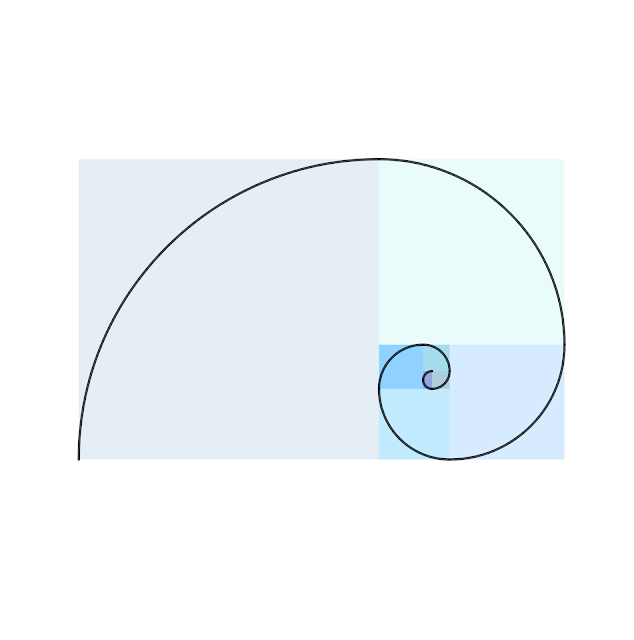
ESPIRAL DE FIBONACCI

Podemos representar a través de una espiral la sucesión de Fibonacci. Pero, lo bonito es saber cómo se elabora esta espiral. ¿Y cómo se elabora? Pues te lo cuento en Geogebra:
Lo podemos hacer de dos maneras: desde un cuadrado de lado 1 (lo más fácil) o calculando las proporciones áureas de cada rectángulo (un poco más difícil). Lo haremos de la primera manera, ya que hablaremos de la segunda en otra ocasión.

CUADRADO DE LADO 1

ANTES DE EMPEZAR: la herramienta para crear polígonos regulares en Geogebra crea los rectángulos hacia arriba si tocas primero en el punto izquierdo y luego en el derecho, si lo haces del revés, lo creará debajo.

1º paso: Lo primero será poner dos puntos con separación de 1.

2º paso: Después de poner los dos puntos, haremos un polígono regular (con la herramienta "Polígono regular" de Geogebra) pinchando en ambos puntos y diciendo que queremos el polígono de 4 vértices (en este caso lo hacemos hacia debajo).


3º paso: Ahora hacemos otro polígono regular con 4 vértices justo encima, con base en los dos puntos azules (hacia arriba).


4º paso: A continuación haremos un cuadrado al lado con referencia en los puntos de la derecha (tocamos primero en el de arriba y luego en el de debajo).


5º paso: continuamos creando cuadrados, en este caso, con referencia en los dos puntos de arriba.


6º paso: Repite tantas veces como quieras el anterior paso, cada vez que lo repitas, estás aumentando un número de la sucesión de Fibonacci.

7º paso: Cuando ya tengas tantos cuadrados como quieras, haremos las circunferencias para representar la espiral. El centro de cada arco de circunferencia ha de ir en una esquina, formando un bucle. El centro del primer cuadrado será la esquina inferior derecha, del segundo la esquina superior derecha, del tercero la esquina superior izquierda, del cuarto la esquina inferior izquierda... Repitiendo siempre ese orden. Lo haremos con la herramienta "Arco de circunferencia".


8º paso: Ahora solo nos queda la decoración. Ocultaremos todos los elementos menos los arcos de circunferencia. Además, ocultaremos la cuadrícula. Antes de hacerlo, podemos tomar como referencia los puntos de las esquinas para hacer un rectángulo, el cual no ocultaremos.



Ahora ya tendrías tu propia espiral de Fibonacci, tan grande como quieras. Puedes dejar si quieres los cuadrados de la elaboración para poder verla mejor, pero es opcional.

SUCESIÓN DE FIBONACCI EN PYTHON

Con el siguiente programa podemos calcular tantos números como quieras de la sucesión de Fibonacci.


Como es costumbre, explicaré el código parte por parte:

1. Crea una variable que tendrá el valor de la respuesta a "¿Hasta qué número quieres saber?". La variable se llamará "n".

2 y 3. Crea dos variables llamadas "n1" y "n2". Estas serán las que se sumen para ir haciendo la sucesión. Esto tiene una explicación, dependiendo de la posición del número en la sucesión, lo dirá n1 o n2, sería tal que así:
Los números en rojo son los que abarcará n1, mientras que los números en verde los abarcará n2. Por ejemplo, 2 es igual a 1 + 1, es decir, a n1 y n2. Esto es lo que ocurrirá en las líneas 10 y 13.


4. Establece un contador a 0. Es una variable llamada "cont".

5. Escribe el número de vez (valor de contador) seguido de ":" y seguido del número correspondiente a la primera vez.

6. Añade uno a contador, diciendo que pasamos de vez.

7. Escribe el número de vez (valor de contador) seguido de ":" y seguido del número correspondiente a, en este caso la segunda vez.

8. Repetirá las líneas 9, 10, 11, 12, 13 y 14 tantas veces como n/2-1 truncado sea. Lo que hace esto es lo siguiente, como en el programa de debajo, por cada repetición escribiremos dos números, los partimos de dos. Luego, le restamos uno al resultado final ya que empieza en 0 las repeticiones, es decir, repetiremos una vez más de no ser por esa resta. Y al final lo truncamos, ya que un número dividido entre dos puede dar decimales y no funcionar el programa. Esa 0.5 significa un número más, lo cual solucionaremos a partir de la línea 15.

9. Añade uno a contador, diciendo que pasamos de vez.

10. Hace que el número 1 sea la suma del mismo número 1 antes de ser sumado y del número 2. Por ejemplo, en la tercera vez (cuando cont = 3), n1 + n2 = 2, por lo tanto, el nuevo n1 será 2. Esto está un poco más explicado en las líneas 2 y 3.

11. Escribe el número de vez (valor de contador) seguido de ":" y seguido del número correspondiente a la vez (n1).

12. Añade uno al contador, diciendo que pasamos de vez.

13. Hace que el número 2 sea la suma del mismo número 2 antes de ser sumado y del número 1. Por ejemplo, en la cuarta vez (cuando cont = 4), n1 (2) + n2 (1) = 3, por lo tanto el nuevo n2 será 3. Esto está un poco más explicado en las líneas 2 y 3.

14. Escribe el número de vez (valor de contador) seguido de ":" y seguido del número correspondiente a la vez (n2).

15. Si la división de n entre 2 no es entera, se ejecutarán las siguientes líneas. Esto es para suplir el truncado de la línea 8. Si por ejemplo la división da algo coma 5, eso es un número más, por lo tanto, hay que escribir otro número de la sucesión más.

16. Añade uno al contador, diciendo que pasamos de vez.

17. Hace que el número 1 sea la suma del mismo número 1 antes de ser sumado y del número 2. Por ejemplo, en la tercera vez (cuando cont = 3), n1 + n2 = 2, por lo tanto, el nuevo n1 será 2. Esto está un poco más explicado en las líneas 2 y 3.

18. Escribe el número de vez (valor de contador) seguido de ":" y seguido del número correspondiente a la vez (n1).

PEQUEÑA DEMOSTRACIÓN DEL PROGRAMA





AMPLIACIÓN: 


Alfredo G. (@alfgoralo) compartió estos dos tweets sobre la sucesión de Fibonacci. Uno contiene una demostración en Geogebra junto a un programilla en Python, mientras que el otro contiene el Geogebra junto a un programilla en JavaScript esta vez. Echadles un vistazo... ¡Son muy chulos! ¡Muchas gracias por dejarme compartirlo!

 

"¡Oh, Leonardo de Pisa!, cuan sabio fuiste introduciendo en Italia la luz de la práctica aritmética." - Antonio de Manzini

Comentarios

Publicar un comentario