CÓMO CALCULAR LA RAÍZ CUADRADA DE UN NÚMERO POR 10

 Ayer, por la noche, sin saber muy bien por qué, descubrí lo siguiente:

√(a * 10) ≈ √a * 3.162...

Viendo esto seguramente te hayas quedado como estabas, pero ahora viene la segunda parte del artículo: LA DEMOSTRACIÓN. Para demostrar algo matemático que sea muy tedioso el calcular, ¿Qué mejor que utilizar la computación? Utilizaremos Python para demostrar que esto es real.

Antes de ello, vamos a hacer un par de comprobaciones propias:

Siendo a = 50, √(50 * 10) = √500 ≈ √50 * 3,162... ≈ 7,071... * 3,162... ≈ 22,358...

Para saber si un número es aproximadamente la raíz cuadrada de otro, bastará con elevarlo al cuadrado. 22,358... ^ 2  ≈ 499,88

Claro, hay que tener en cuenta que para hacer este cálculo nos hemos dejado una barbaridad de decimales, pero, a pesar de ello, hemos conseguido acercarnos muchísimo al número real. No obstante, eso no pasará en nuestra demostración en Python. ¡Vamos allá!

Este va a ser nuestro primer mini programa.

1. La primera línea importa de la librería math la instrucción sqrt que nos hará raíces cuadradas.

2. Esta línea designa el número a sobre el que todo girará.

3. Esta línea calcula la raíz cuadrada de solamente el número a y la guarda en una variable que se llama rcA (Raíz Cuadrada de A).

4. Esta línea implementa la fórmula que comentamos anteriormente para calcular la raíz cuadrada de a*10.

5. Esta línea eleva al cuadrado la supuesta raíz cuadrada de a * 10 y lo guarda en una variable que se llama b.

5. Imprime (escribe) el valor de la variable rcAx10 (Raíz Cuadrada de A por (x) 10).

6. Imprime (escribe) el número a * 10 según la supuesta raíz cuadrada que hemos calculado.

Lo que nos devuelve este programa es esto:

(El primer finished... es un error anterior)

Como vemos, se acerca un poco más a 500 (50*10) que el cálculo que hicimos nosotros antes. Vamos a hacer que se aproxime todavía más.

La pregunta del millón es cómo he conseguido ese 3,126... Ese es el número que se obtiene al dividir la raíz cuadrada de a*10 entre la raíz cuadrada de a. Este número tiene muchos decimales con los que, nosotros, humanos, no vamos a operar. Pero, la computación, sí.

Con este programa que tenemos aquí podremos hallar el número 3,126... de una manera mucho más completa.

1. Importamos la instrucción de la raíz cuadrada.

2. Asignamos a a el valor 50 (igual que antes).

3. Asignamos a b el valor a * 10.

4. Asignamos a n el resultado de la división entre la raíz cuadrada de b (siempre mayor que la de a) y la de a.

5. Imprimimos (escribimos) el valor de n.

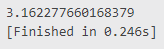
Esto es lo que nos devuelve el programa. Ya tenemos un número mucho más exacto con el que trabajar.

Vamos a probar a juntar los dos programas. El segundo para tener el número con el que multiplicar mucho más completo y el primero para implementar la fórmula.

Este programa sería el resultante de juntar ambos anteriores.

1. Importamos otra vez la instrucción para obtener raíces cuadradas.

2. Asignamos a a un valor que en este caso es 50 (por ejemplo).

3. Asignamos a b el valor a * 10.

4. Asignamos a n el resultado de la operación de la raíz cuadrada de b entre la raíz cuadrada de a. Este número es el comentado anteriormente 3,162...

5. Asignamos nuevamente a a un valor. Este valor es sobre el que aplicaremos la fórmula. Por ejemplo, el valor será 13 589.

6. Asignamos a la variable rCa (Raíz Cuadrada de A) el valor de la raíz cuadrada de a.

5. Asignamos a la variable rCb_aX10 (Raíz Cuadrada de B que es A por (X) 10) el resultado de multiplicar la raíz cuadrada de a por el número conseguido en la línea 4, lo que viene siendo nuestra fórmula.

6. Imprimimos (escribimos en consola) la supuesta raíz cuadrada de a * 10.

7. Asignamos a la variable b el valor de elevar la raíz cuadrada de b al cuadrado.

8. Imprimimos el supuesto número b.

Ahora vamos a verlo en acción:

Según el programa, sin hacer en ningún momento ninguna raíz cuadrada al número a * 10, la raíz cuadrada de este es 368,... Además, sin hacer en ningún momento la operación de multiplicar por 10 el número a, sabemos que a * 10 es 135890.

¡Espero que hayas disfrutado leyendo este artículo tanto como yo escribiéndolo!